Optimal and Robust Control

Get a boat as far as possible

Find the optimal control policy getting a boat in a river stream as far as possible. The equations of motion of the boat in the river stream are

The boat is at time \(t=0\) located on a river bank (i.e. \([x(0),y(0)]=[0,0]\)). The only way how you can influence the motion of the boat is via commanding the angle \(\theta\).  

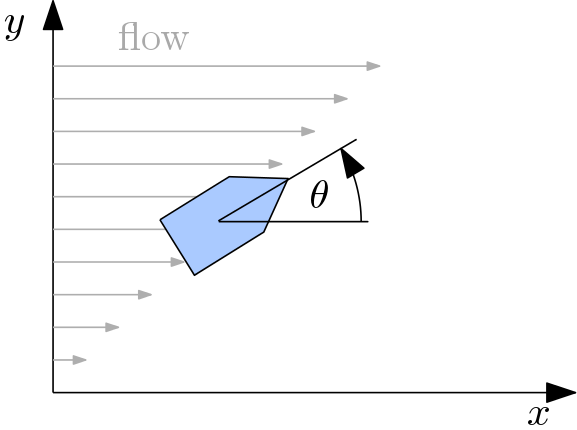
Your goal is to get the boat as far possible along the x-axis during a fixed time interval [0,5].

Implement your solution as a function with the header of the following form:

function [ t_star, x_star, u_star ] = hw7_cvutID()

where cvutID is your KOS username, t_star is the time vector of the trajectory, x_star is the state trajectory and u_star is the control trajectory. You are free to choose the sampling of the time interval [0, 5]; in other words, time samples in t_star can be arbitrarily spaced.

Note that the parameters of the flow field are not the same as you had in the first round of this homework assignment. This time, the flow field depends quadratically on the y coordinate as opposed to linear dependence you had before. This little change makes the problem way more challenging to solve analytically and thus we encourage you to use a numerical solver (like bvp4c) in Matlab instead. Numerical solvers are quite often very sensitive to initial conditions. Try more initial conditions and submit the solution with the initial condition resulting in the best performance (=largest final-time coordinate x).

You can submit only one m-file. If you need more functions, you can use nested functions (for details, see this).