Optimal and Robust Control

Inverse Kinematics Problem by Quasi-Newton Methods

Solve numerically the inverse kinematics problem for the 4-link planar robot visualized in the figure below. Inverse kinematics problem is a problem where you are given a position of the end effector (e.g. a gripper) of a robot and your goal is to find such joint coordinates—for instance, angles in case of rotational joints—that the robot's end effector ends up in the required position. Without delving into details, let us state that some inverse kinematics problems have closed-form solutions (you can solve them analytically) and some do not. For the latter case, you have to invoke numerical methods. That is exactly what you will be dealing with in this homework assignment.

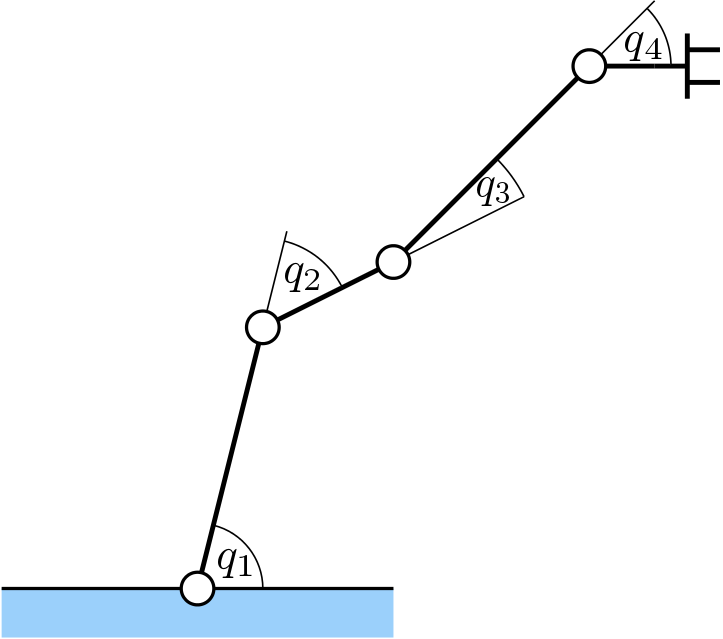
There are more ways how to solve numerically inverse kinematics problems, nevertheless, you are required to solve the particular problem of this homework assignment by the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm. This algorithm belongs to the family of so-called quasi-Newton methods which do not compute the Hessian of the objective function exactly (as opposed to Newton methods) but only approximatively based on the gradient of the objective function (which can be estimated by numerical differentiation, if not available). Even though this algorithm was not covered in today's lecture, you shouldn't have any problems to learn it by yourself.

Download the attached hw2_cvutID.m file and get familiar with the code in it. All the supporting function—like a plotting function, forward kinematics function, and objective function—has been already implemented. The only missing part is an implementation of the BFGS algorithm. Hence, your task is to implement the BFGS algorithm to the attached hw2_cvutID.m, replace cvutID in the name of the file and the name of the main function by your actual KOS username, and submit the modified file as the solution of this homework assignment. You can submit only one m-file. If you need more functions, you can use nested functions (for details, see this).