Optimal and Robust Control

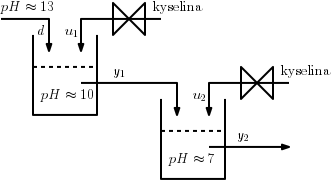
Consider the neutralization process in the figure above where acid is added in two stages. Most of the neutralization takes place in tank 1 (left) where a large amount of acid is used (input \(u_1\)) to obtain a pH of about 10 (measurement \(y_1\)). In tank 2 the pH is fine-tuned to about 7 (output \(y_2\)) by using a small amount of acid (input \(u_2\)). This description is just to give you some idea of a real process; all the information you need to solve the problem follows.

A block diagram of the process is shown in the figure below. It includes one disturbance \(d\), two inputs \(u_1\) and \(u_2\) and two measurements \(y_1\) and \(y_2\). The diagram represents a deviation model from a desired operating point, i.e. both the inputs and outputs are ideally zero. The main control objective is to keep \(y_2\approx 0\). In addition, we would like to reset input 2 to zero; that is, we want \(u_2 \approx 0\) at low frequencies. Note that there is no particular control objective for \(y_1\).

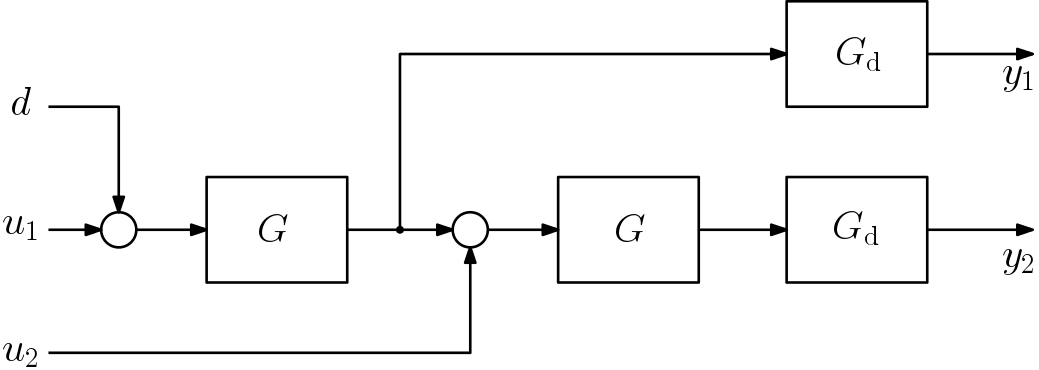
The transfer functions are

Your task is to formulate the control design problem as a general \(H_\infty\) norm minimization problem and find a controller minimizing \(H_\infty\) norm of an appropriate transfer function. Specifically, this problem is an instance of signal-based \(H_\infty\) control. For details about this control design approach see lecture notes (slides) for this week or documentation for Matlab function hinfsyn(). Even more details can be found in Chapter 9 (especially the introduction of 9.3 and sections 9.3.5 and 9.3.6) in Multivariable Feedback Control by Skogestad and Postlethwaite. 

Notice that the transfer function \(G_\mathrm{d}\) represents the transportation delay of the measurement. As transportation delay might cause some problems when used with hinfsyn(), approximate \(G_\mathrm{d}\) during the design process by Pade approximation (see 'doc pade' in matlab). Nevertheless, you should test your controller on the original model without any approximations.

Download the attached m-file and fill in the gaps or missing lines in the code. Submit the updated code.